最近ショート動画なんかで、この「行き時速40km、帰り時速60kmの平均時速は?」という動画がまわってきましたw さて、この答えなんだと思いますか?w
この問題をパッと見で答えると、平均なんで足して2で割るでよくね?って考えるかもですw
(40+60)÷2=50 50kmです!
というわけなんですが、間違いですw 解き方はここでは説明しませんが、答えは、
時速48km
です。この問題での平均時速を計算するためには、走った距離を時間で割るということでしか求められないわけなんですが、同じ速さでない場合には、足して2で割った値(この場合50km)から遅い方の速さに引きずられるというのが「平均」になります。この考え方が「加重平均」とか「調和平均」と言われます。
なぜこのようなことを話題にしたのか?といいますと、構造を理解して安定的な構造を作り上げるというのは、この「加重平均」とか「調和平均」というものがしっかり理解できていないとダメなのです。また、構造計画を行うときの「肝」になるのもこの点です。例えば、2階からの荷重を1階の柱が受け持つことを考えてみましょう。
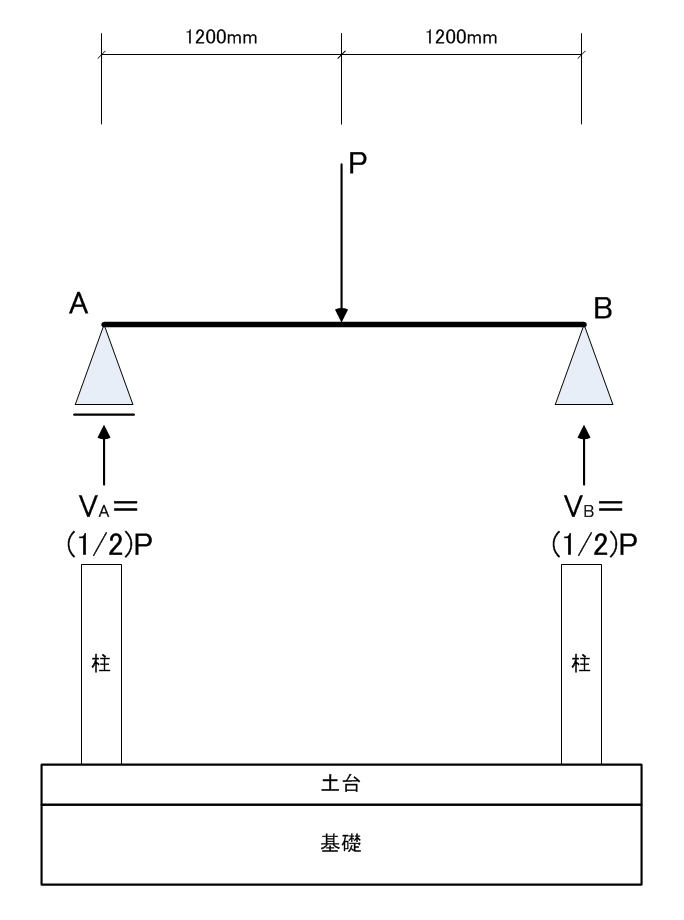
柱と柱の真ん中(中心)にポツンと荷重Pをかけた場合には、両端の柱が受け持つ荷重は「半分こ」になりますw (1/2)Pってわけです。ところが、これがちょっとずれたらどうなるか?というと、例えば、以下の図のようになると、
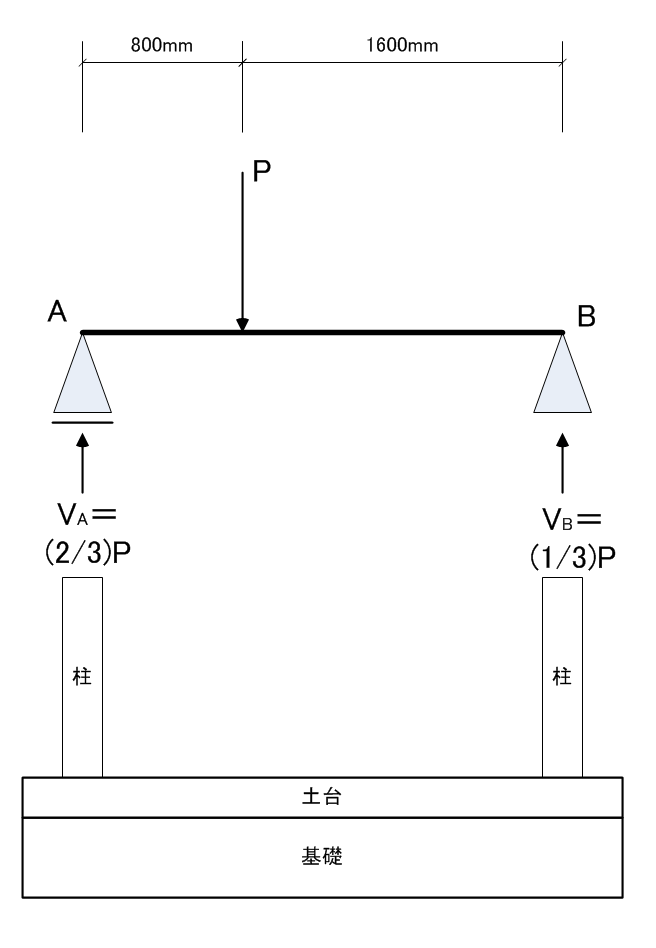
どちらかの柱が受け持つ荷重が大きくなるわけです。これを「偏り」といいます。ちなみに荷重Pは「2階の柱」になることが多いです。言い換えますと、2階の柱が1階の柱の中間部にある場合、その位置によっては1階の柱にかかる荷重Pの大きさが「変わる」というわけです。
当たり前なことですが、上図の場合、左側のVAのほうが大きいわけですので、大きな耐力を必要とする場所は、Aの側に寄っていくことになります。この「偏り」が建物の安定性に影響を与えるかどうか?が構造計画の「肝」というわけです。
実は、冒頭の速度の平均の問題と同じような数学的な感覚がこの構造計画においても求められます。この「荷重の伝達の割合」を自由にコントロールできるようになると、自由な構造計画が可能になっていきます。


